서론
현재 Reverie의 물리엔진은 매우 느리다.
구체적으로 말하자면, 어떤 블럭 A를 밀 수 있는지 판별하기 위해서 지수함수적 시간이 걸리는 알고리즘을 사용한다.
(n은 맵의 움직일 수 있는 블럭의 수)
이는 맵에 움직일 수 있는 물체가 많아질수록, 최악의 경우 게임이 기하급수적으로 느려지게 된다는 것을 의미한다.
(즉, 블럭 하나를 추가할 때마다 게임이 2배씩 느려지는 현상이 발생할 수 있다)
이 글은, Reverie에서 어떤 블럭을 밀 수 있는지 판별하는 알고리즘은 반드시 지수함수적 시간이 걸릴 수밖에 없음을 증명하는 내용이다.
(P != NP를 가정. 앞으로 이 가정은 생략한다)
* 물론, 사실 대부분의 맵에서 움직일 수 있는 물체의 수는 5개 이하이다... 그런 맵에서 렉이 걸리는 경우 원인은 이 글에서 분석한 이유와 전혀 상관없을 가능성이 크다.
즉, 이 글은 어디까지나 이론적인 분석을 다룬 글이며, 실제로 Reverie가 느리다면 그것은 아마 구린 코딩이 원인일 것이다.
문제 정의
Reverie의 규칙을 간단히 소개한다. (구체적인 내용은 다른 포스트 참고)
0.0 검정 블럭과 흰 블럭이 존재한다.
0.1 모든 블럭은 '고정 블럭' 이거나 '이동 가능 블럭' 둘 중 하나이다.
1.0 블럭끼리 겹치는 경우, 서로 다른 색의 블럭끼리만 맞닿을 수 있다. (아래 참고)

물체를 색종이로 생각하면 편하다. 같은 색 색종이끼리 닿아 있는 상황은 불허된다.
부가 설명)
위쪽 상황은 두 물체가 낑긴(?) 것으로, 발생하면 안 되는 상황.
아래 상황은 흰색 물체를 배경으로 이해하면, ㄱ 모양 물체와 ㅁ 모양 물체가 서로 떨어져 있는 상황.
1.1 다음 상황을 만족할 때 블럭을 밀 수 있다.
구체적으로)
블럭 A를 오른쪽으로 1 픽셀 밀 수 있다 =
블럭 A를 오른쪽으로 1픽셀 이동시키고, 원한다면 다른 블럭들도 오른쪽으로 1픽셀 이동시켜서, '허용되는 상황'을 만들 수 있다.
(이때, '고정 블럭'은 이동할 수 없다)
1.1-2 이때, 블럭이 이동함에 따라 블럭끼리 겹치게 되는 경우가 있다. 이 경우 '허용되는 상황'을 위해 겹친 블럭끼리의 순서를 자유롭게 지정할 수 있다. (아래 참고)

위 그림의 왼쪽 상황에서 검정 블럭을 완전히 겹쳐진 3개의 물체 쪽으로 미는 것을 생각해 보자.
검정 블럭은 흰색 블럭의 뒤쪽으로 갈 수도 있고, 앞쪽으로 갈 수도 있다.
위 그림에서 1) 오른쪽 위는 블럭이 뒤쪽으로 간 상황이며, 2) 오른쪽 아래는 블럭이 앞쪽으로 간 상황이다.
증명 방식
널리 알려진 문제 중 'SAT'라는 문제는 풀기 위한 알고리즘이 반드시 지수함수적 시간이 걸림이 증명되어 있다.

SAT는 위처럼 and, or, not으로 이루어진 식이 주어지면, 변수 A, B, C ... 에 True/False 를 대입해서 식을 True로 만들 수 있는가? 를 묻는 문제이다.
* 이제부터 다음과 같이 줄여 쓰겠습니다:
Reverie 물리엔진 = Reverie의 블럭이 밀리는지 판별하는 알고리즘
따라서 Reverie 물리엔진을 1회 사용해서 SAT를 풀 수 있음을 보이면,
이는 Reverie 물리엔진이 지수함수적 시간이 걸릴 수밖에 없다는 증명이 된다.
여기서 일반적인 SAT의 경우 식의 형태가 아무거나 될 수 있어서 표현이 쉽지 않다.
그러나 식의 정리를 통해, 어떤 식이든 훨씬 처리가 용이한 '정리된 형태'로 바꿀 수 있다는 것이 밝혀져 있다.
사실 위의 예시 또한 '정리된 형태'의 식인데, 이는 다음과 같은 형태를 의미한다.
(OR로만 묶인 절) AND (OR로만 묶인 절) AND (OR로만 묶인 절) AND ...
NOT의 경우에는 식에 사용하지 못하고 ~A 이런 식으로 개별 변수에만 붙일 수 있다.
이 '정리된 형태'의 식을 CNF라고 부른다.
모든 식은 CNF로 바꿀 수 있으니, 우리는 CNF에 대한 답만을 구해주면 된다.
혹시 boolean의 개념에 익숙하지 않다면, 아래 링크 참고
https://math.stackexchange.com/questions/86210/what-is-the-3-sat-problem
증명 - 게이트 구성
1. OR 게이트
아래 그림과 같은 상황을 생각해 보자.

위의 규칙에서 설명했듯이, X라는 물체를 밀면 A가 밀릴 수도 있고 B가 밀릴 수도 있다.
이는 다음과 같이 생각할 수도 있다.
X를 밀 수 있을 조건 = 'A를 밀 수 있다' OR 'B를 밀 수 있다'
따라서 위는 OR게이트의 역할을 수행하게 된다. 이는 나중에 회로가 완성된 모습을 본 후에 더 이해가 쉬울 수도 있다.
2. XOR 게이트
XOR 게이트는 OR 게이트와 거의 똑같게 생겼다.
다만, 흰 물체가 '고정 상태'라는 점이 다르다.
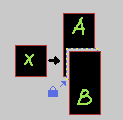
이 상황에서 A와 B를 '동시에' 미는 것은 불가능하다.
왜냐하면 흰색 물체의 오른쪽에서 A와 B가 겹치게 되고, 이는 불허된 상태이기 때문이다.
따라서 이 경우 X를 밀면 A, B중 정확히 한 개만 밀려야 한다.
이 게이트의 활용성은 지금은 이해하기 힘들 텐데, 나중에 회로가 완성된 모습을 보면 이해가 쉬울 것이다.
* 여기서 '고정 물체' 뒤쪽으로 '이동 물체' 가 이동하는 것이 규칙상 허용되는가? 라는 의문을 가질 수도 있다.
결론부터 말하자면, 이는 허용된다. (허용된 이유 또한 있다)
그러나 이것이 XOR게이트의 구성에 필수적이진 않다.
'고정 물체'가 무조건 뒤에 있는 XOR게이트 또한 만들 수 있으나, 더 구조가 복잡하여 위 형태를 가져왔다.
3. AND 게이트
AND 게이트는 워낙 단순해서 별다른 설명이 필요 없다.
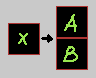
X를 밀 수 있을 조건 = 'A를 밀 수 있다' AND 'B를 밀 수 있다'
위 그림처럼 A, B를 세로로 배치해도 되지만, 가로로 나란히 둬도 된다.
4. 전선
A라는 블럭이 밀렸다는 사실을 먼 곳까지 전달하기 위해서는 전선(wire)이 필요하다.

위 그림을 보자.
우선 당연히 A가 밀린다면, 반드시 B도 밀린다.
덜 자명한 점은, B가 밀린다면, 반드시 A도 밀린다는 점이다.
이는 사실, 배경엔 거대한 흰색 물체가 하나 있기 때문이다.
중간의 흰색 물체 아래쪽이 커버되지 않는다면 배경과 중간의 흰색물체가 닿게 되고,이는 불허된다.
전선 예시)

5. 전선 교차
두 개의 독립적인 전선이 서로 교차할 필요가 있을 때가 있다.

이때는 위와 같이 교차한 부분 사이에 딱 겹치는 만큼의 크기의 흰색 물체를 넣으면,
두 전선이 서로에게 영향을 주지 않고 잘 동작한다.
증명 - 회로 구성
이제 우리는 회로를 구성할 준비가 다 되었다.
Step 1. 변수의 값 설정
다음과 같이 세 변수 A, B, C를 쓰는 식을 생각해 보자.

* 축약 표기) ~
~A = not A
변수 A의 경우, A 또는 ~A 둘 중 정확히 하나만이 성립해야 한다. 우리는 이를 XOR게이트로 구현한다.

참고) 그림상에선 블럭 간에 간격이 있지만, 실제로는 모두 긴격 없이 붙어 있다.
즉, X를 1픽셀 미는 순간 C구역 블럭까지 모두 1픽셀 밀려야 한다.
X를 1픽셀 미는 순간, A 또는 ~A가 1픽셀 밀리고, B 또는 ~B가 1픽셀 밀리고, C또는 ~C가 1픽셀 밀린다.
예를 들어 A, ~B, C가 밀린 경우, 이는 A = True, B = False, C = True 라는 변수 값이 설정된 것이라고 해석하면 된다.
Step 2. OR로 이루어진 절 구성
우선 예시 식의 첫번째 항, (A \/ B) 를 표현해 보자.
위의 XOR 회로 위쪽에 A \/ B를 추가하면 된다.
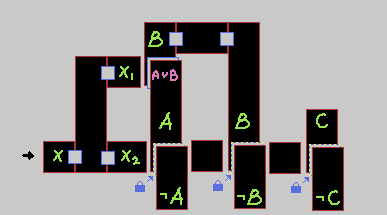
X가 밀리기 위해서는 X1 과 X2 가 모두 밀려야 한다.
1. X2는 XOR 게이트 부분을 밀면서 (A 또는 ~A), (B 또는 ~B), (C 또는 ~C) 중 하나씩만을 밀어야 한다.
2. X1은 OR 게이트 부분을 밀어야 하는데, 그러기 위해서는 A가 밀려있거나, B가 밀려있어야 한다. (둘 다 밀려있어도 OK)
이때, 1. 에서 ~A 와 ~B를 밀어버렸다면 A와 B 둘 다 밀 수 없어서 모순이 발생.
따라서 1. 에서 A와 B중 하나는 반드시 밀었어야 했다.
Step 2-2. OR로 이루어진 절 구성 (변수 3개)
이번에는 (~A \/ B \/ C)를 표현해 보겠다.
(~A \/ B \/ C) = ~A \/ (B \/ C) 이므로 OR 게이트를 2개 쓰면 된다.
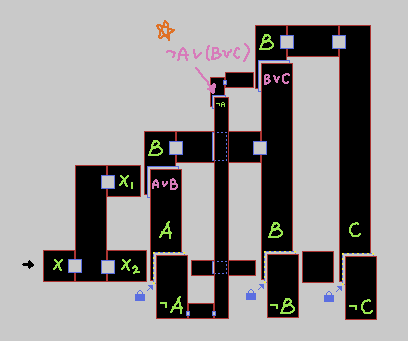
주황색 별표가 있는 곳이 (~A \/ B \/ C) 이다. X에는 연결이 안 되어 있는데, 이는 바로 다음 스텝에서 진행한다.
Step 3. AND로 이루어진 절 구성
AND 추가는 매우 단순하다.
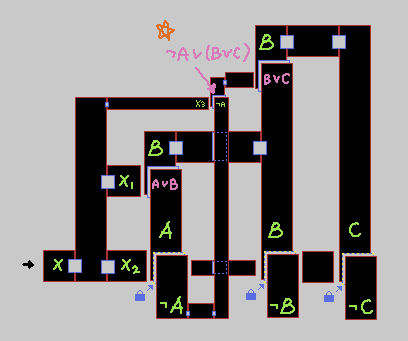
X3가 추가되면서 AND역할을 수행한다.
이제 이 상태에서 다음이 성립한다.
X가 밀릴 조건 = (A \/ B) /\ (~A \/ B \/ C) 의 해가 존재한다
결론
같은 원리로 임의의 CNF 식을 블럭 배치로 표현 가능하다.
이는 Reverie 물리엔진을 1회 사용해서, 그 결과를 보고 CNF 식이 답이 있는지를 알 수 있다는 뜻이다.
결론: Reverie 물리엔진은 지수함수적인 시간 복잡도를 가져야 한다.
사실, 엄밀한 증명을 위해서는 회로를 만들기 위해 사용하는 블럭 수가 너무 많지 않다는 것 또한 증명해야 한다.
그러나 이 갯수 재한은 매우 널널하다.
길이 L인 식을 표현하기 위해 f(L)개의 블럭을 사용한다고 할 때, f(L)이 다항함수이기만 하면 된다.
이는 매우 약한 조건이기에 증명은 생략한다.
별첨
고정 물체'가 무조건 뒤에 있는 XOR게이트는 다음과 같은 모습이다. (3이 완성된 모습)

'유니티 게임 개발 일지' 카테고리의 다른 글
| 인디게임 관련 주요 이벤트 일정 (0) | 2023.08.21 |
|---|---|
| 의욕을 높이는 법에 대해 (1) | 2023.08.21 |
| Pitch Deck 용 설명 이미지 (0) | 2022.06.17 |
| [일지 / 그래픽] 6. 그래픽 인게임 적용 (0) | 2022.02.13 |
| [일지 / 그래픽] 5. 레버리 3번째 컨셉 아트 (도시) (0) | 2022.01.29 |

