Reverie 는 유니티 엔진을 사용하지만, 자체 충돌 처리 시스템을 활용한다.
즉, 유니티에서 제공하는 Collider 기반 충돌 시스템을 사용하지 않는다.
말은 거창하지만, Reverie 에서 현재 지원하는 충돌체는 AABB(한마디로 사각형, 그것도 좌표축에 평행한 것들)밖에 없다.
그리고 두 개의 AABB 가 충돌하는지 판단하는 것은 매우 쉽다...ㅋㅋㅋㅋ
다만 이것이 문제가 되는 경우는, 이러한 충돌체가 많을 때이다.
주황색 영역에 닿는 파랑색 물건의 리스트를 구하는 작업을 생각해 보자.
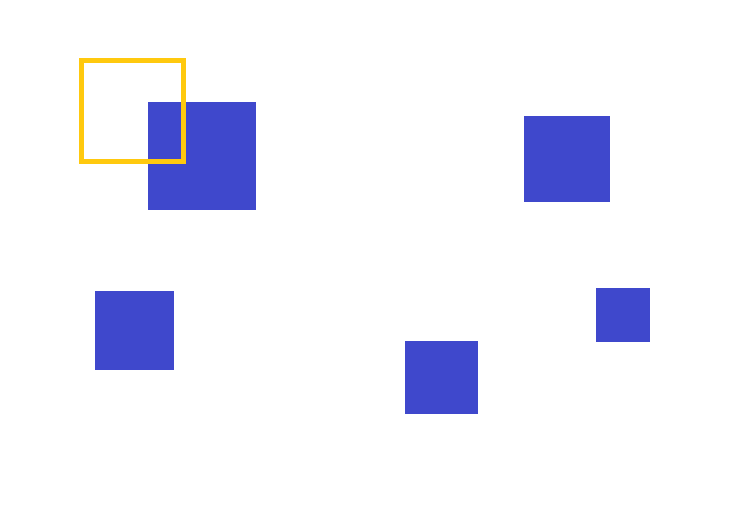
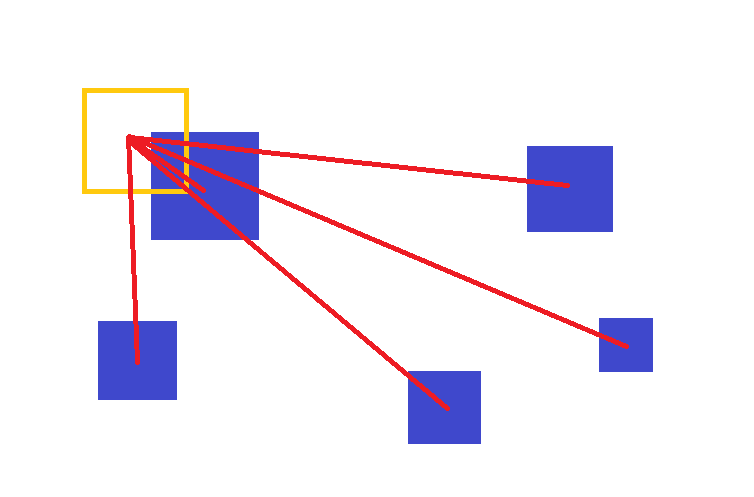
주황색과 각 파랑 물건이 충돌하는지를 체크해야 하므로 총 5번의 계산이 필요하다.
이때 5은 작은 숫자지만, 파랑 물체가 10000개 있다면 10000 번의 계산이 필요하게 될 것이고...
계산량은 파랑 물체의 수에 비례하여 증가하게 된다.
Reverie 의 경우는 물체가 그렇게 많을 것으로 예상하지는 않지만, (최대 200개 정도) 이러한 충돌 체크를 한 프레임 안에도 반복적으로 여러 번 해야 할 것이 예상되기에 최적화 작업을 미리 해 둘 필요가 있다고 생각하였다.
충돌을 효과적으로 체크하기 위한 기법
그렇다면 어떤 식으로 충돌을 효과적으로 체크할 수 있을까?
효과적으로 충돌을 체크하기 위해서는 말도 안 되는 충돌 (엄청 멀리 있다던가...) 들을 미리 걸러내서 이런 경우 아예 충돌 체크를 진행도 하지 말아야 한다.
이때 알고리즘마다 어떤 충돌이 '말도 안 되는지' 체크하는 방식이 다른데, 이중 가장 간단하고 Reverie 에 활용되는 방식을 소개한다.
- 균등한 격자판 활용 (Spatial Hashing) -
주황색 영역에 닿는 파랑색 물건의 리스트를 구하는 작업을 생각해 보자.
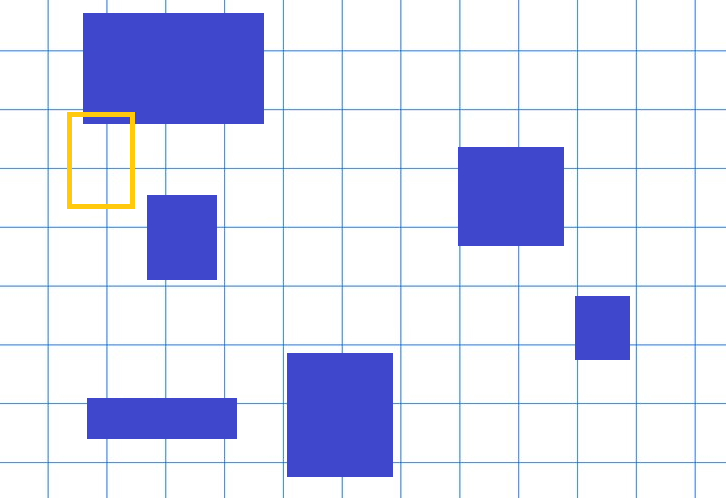
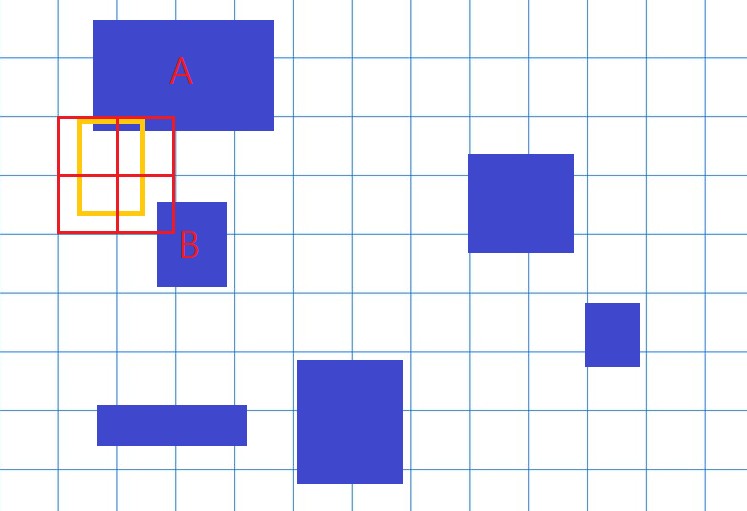
이때 오른쪽의 빨강색 칸은, 격자판의 칸 중에서 주황 물체와 닿는 것들이다.
이때, 파란색 물체 중 '빨간 칸에 안 닿아 있는' 물체들은 모두 주황색과 충돌할 리가 없으므로 체크할 가치가 없다!
따라서 2개의 후보군 A, B 와 충돌체크를 하면 끝난다.
그럼 A는 주황색과 충돌하고, B는 주황색과 충돌하지 않으므로 최종 답은 A.
만일 물건들이 격자 오른쪽으로 10000 개가 더 있었다고 해도 다 무시하고, A, B 하고만 충돌체크를 하면 된다.
- 그러나 다음과 같은 의문이 생길 수 있다.
하지만 파란색 물체 중 빨간 칸에 안 닿아 있는 물체는 어떻게 효율적으로 구하죠?
결국 모든 파랑 물건에 대해 빨간 칸에 닿아 있는지 계산을 해야 하는 것은 마찬가지 아닌가요?
맞는 말이다. 그래서 추가 설명이 약간 필요한데, 맨 처음에 다음과 같은 작업을 해야 한다.
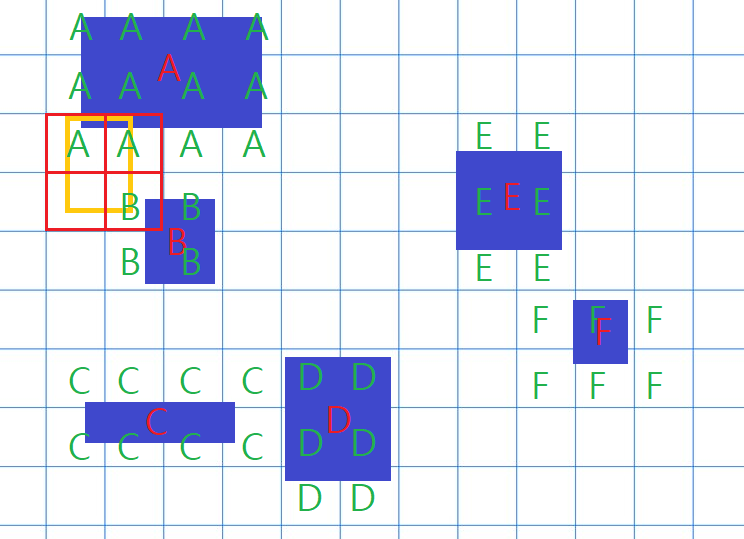
바로 각 칸마다, 자기와 닿아있는 물체의 이름을 적어 두는 것이다.
비록 이 작업 자체는 오래 걸리지만, 한번만 해 두면 앞으로의 충돌체크는 모두 빨라진다.
위 예시의 경우 빨강 칸에 A, A, B 라고만 적혀 있으므로 바로 C, D, E, F 는 빨간 칸과 안 닿아 있다는 것을 바로 알 수 있다.
다음 번의 충돌 체크 때도 다른 칸에 적힌 글자를 보면 바로 해당 칸과 닿아 있는 물체를 알 수 있다.
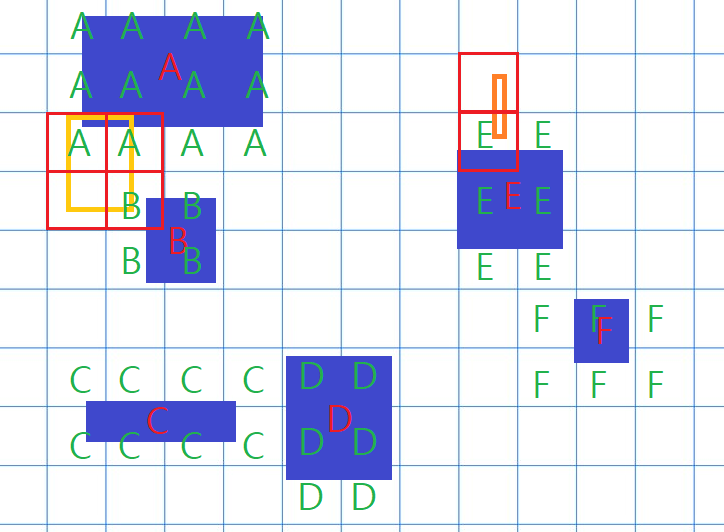
오른쪽에 새로운 진한 주황 네모와의 충돌체크를 진행할 때도, 맨 처음에 적어 두었던 초록 글자를 참고하면 바로 E 가 후보임을 알 수 있다.
* 참고: 예시에선 안 나왔지만, 어떤 칸 하나에 여러 개의 물체가 닿는다면 칸에 "A, B" 와 같이 글자 여럿을 적어야 할 수도 있다.
* 참고 2: 만일 어떤 파랑 물체가 움직여서 딴 곳으로 가 버린다면, 해당 물체에 대한 초록 글자들을 지우고 다시 알맞은 위치에 적어야 한다.
다른 알고리즘들과의 비교
빠른 충돌 체크를 위한 알고리즘은 Spatial Hashing 외에도 QuadTree, BVH 등이 있다.
원래는 이들에 대한 설명도 모두 적을 예정이었으나... 이들 중 제일 간단한 Spatial Hashing 조차도 쉽게 설명하는 데에는 매우 오랜 시간이 걸리는 것을 보고 포기했다.
이미지 편집에 그림판을 활용한 게 제일 큰 문제인 것 같다 ㅋㅋㅋㅋㅋ
하지만 아주 간략하게 개요만 설명해 보도록 한다.
1. 퀴드트리 - QuadTree
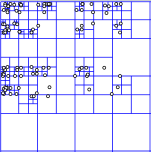
우리가 위에서 본 격자판 기법과 비슷한데, 물체들이 밀집된 부분일수록 격자를 좀 더 촘촘하게 나눴다고 보면 된다.
밀집된 부분을 좀 더 촘촘하게 나눠 주는 만큼, 물체들이 불균일하게 분포될 가능성이 많다면 QuadTree 가 Spatial Hashing 보다 유리해진다.
또한, 충돌체크를 하고 싶은 영역 (주황색 영역) 의 크기가 다양한 경우에도 이점을 가진다.
2. Bounding Volume Hierarchy - BVH
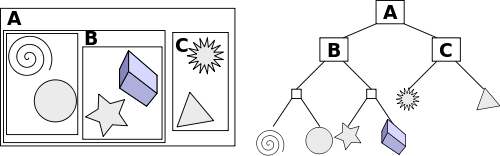
서로 다른 물체들을 묶어서 새로운 큰 덩어리를 만드는 기법. 유니티도 이 방식을 활용한다.
예를 들어 개별 물체와 충돌을 체크하는 대신, C라는 2개의 물체가 뭉쳐진 네모덩어리와 먼저 충돌을 체크한다.
만일 C와 충돌하지 않는다면, C 안에 포함되는 2개의 모양과는 당연히 충돌하지 않을 것이므로 충돌체크를 건너뛸 수 있다!
Reverie 에서의 경우
Reverie 의 경우 타일맵 형식의 게임이기 때문에,
- 대부분의 충돌체가 1타일 크기이다
- 충돌 체크는 대부분 1타일 크기 영역에서 이루어진다
- 매우 충돌체가 균등하게 분포되어 있다 (Reverie 의 특성상 빈 공간에도 충돌체가 있을 예정)
위와 같은 조건을 만족하기 때문에, QuadTree 나 BVH 등 좀 더 복잡한 고급 기능을 활용할 필요가 없었다.
따라서 구현도 가능하고 가벼운 Spatial Hashing 을 사용하였다.
Source Code (Spatial Hashing)
Spatial Hashing 이 이미 구현된 것을 인터넷에서 찾아보려 했으나, Unity 용으로 딱 알맞는 코드를 찾을 수 없었다.
Spatial Hashing 은 비교적 구현이 간단하므로, 직접 구현해 보았다. (Unity, int 좌표용)
아마 특수한 상황이 아니면 int 만 지원하는 spatial hashing 이 필요 없겠지만... 쓰고 싶다면 자유롭게 사용하기 바란다.
굳이 명확하게 하기 위해 라이센스도 표기하자면, CPOL 라이센스 하에 공유하겠다.
(어떤 방식으로든 자유롭게 사용 가능, 오류 등에 대해 원작자에게는 책임 없음)
https://www.codeproject.com/info/cpol10.aspx
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using System.Linq;
using System;
namespace CustomCollection
{
public interface IHasRect
{
RectInt Rectangle { get; }
}
public class SpatialHashMap<T> where T : IHasRect
{
/// <summary>
/// Construct a spatial hashMap
/// </summary>
public SpatialHashMap()
{
}
public SpatialHashMap(IEnumerable<T> enumerable)
{
foreach (var elem in enumerable)
{
Add(elem);
}
}
/// <summary>
/// Width and height of a single grid, expressed in log base 2.
/// Actual Width and height values = 2 ^ gridSize.
/// </summary>
private int gridSize = 5;
private Dictionary<Vector2Int, List<T>> dict = new Dictionary<Vector2Int, List<T>>();
private Dictionary<T, List<Vector2Int>> reverseDict = new Dictionary<T, List<Vector2Int>>();
public void Add(T elem)
{
var rect = elem.Rectangle;
foreach (var key in GetKeysForRect(rect))
{
AddToKey(key, elem);
}
}
private void AddToKey(Vector2Int key, T elem)
{
if (!dict.ContainsKey(key))
dict[key] = new List<T>();
var lis = dict[key];
if (!lis.Contains(elem))
lis.Add(elem);
if (!reverseDict.ContainsKey(elem))
reverseDict[elem] = new List<Vector2Int>();
var reverseLis = reverseDict[elem];
if (!reverseLis.Contains(key))
reverseLis.Add(key);
}
public List<T> GetElementsMeetingRect(RectInt rect)
{
List<T> lis = new List<T>();
foreach (var key in GetKeysForRect(rect))
{
ConcatToList(lis, key, rect);
}
return lis;
}
private void ConcatToList(List<T> lis, Vector2Int key, RectInt rect)
{
if (!dict.ContainsKey(key))
return;
var toConcat = dict[key].Where(e => !lis.Contains(e) && RectIntersects(rect, e.Rectangle));
lis.AddRange(toConcat);
}
public void UpdateElem(T elem)
{
if (!reverseDict.ContainsKey(elem))
{
Add(elem);
return;
}
var revDict = reverseDict[elem];
var rect = elem.Rectangle;
var keys = GetKeysForRect(rect);
bool valid(Vector2Int pos) => keys.Contains(pos);
foreach (Vector2Int pos in revDict)
{
if (!valid(pos) && dict.ContainsKey(pos))
{
dict[pos].Remove(elem);
}
}
revDict.RemoveAll(e => !valid(e));
foreach (var key in GetKeysForRect(rect))
AddToKey(key, elem);
}
private IEnumerable<Vector2Int> GetKeysForRect(RectInt rect)
{
int xStart = rect.xMin >> gridSize;
int xEnd = (rect.xMax - 1) >> gridSize;
int yStart = rect.yMin >> gridSize;
int yEnd = (rect.yMax - 1) >> gridSize;
for (int x = xStart; x <= xEnd; x++)
for (int y = yStart; y <= yEnd; y++)
yield return new Vector2Int(x, y);
}
public static bool RectIntersects(RectInt a, RectInt b)
{
var res = RectIntersection(a, b);
return res.width > 0 && res.height > 0;
}
public static RectInt RectIntersection(RectInt a, RectInt b)
{
var xMin = Mathf.Max(a.xMin, b.xMin);
var yMin = Mathf.Max(a.yMin, b.yMin);
var xMax = Mathf.Min(a.xMax, b.xMax);
var yMax = Mathf.Min(a.yMax, b.yMax);
return new RectInt(xMin, yMin, xMax - xMin, yMax - yMin);
}
}
}'유니티 게임 개발 일지' 카테고리의 다른 글
| [일지 / 그래픽] 5. 레버리 3번째 컨셉 아트 (도시) (0) | 2022.01.29 |
|---|---|
| [일지 / 개발] 4. Reverie 에 Undo 시스템 추가 (0) | 2022.01.15 |
| [일지 / 그래픽] 3. 레버리 2번째 컨셉 아트 (정글) (0) | 2021.08.27 |
| [일지 / 기획] 2. Reverie 의 작동 원리 (0) | 2021.08.25 |
| [게임 개발 일지] 0. 과거 Reverie 의 모습 / 앞으로의 계획 (0) | 2021.08.17 |


